【Coding】算法题编程记录

References

二分查找

概念

二分查找的做法：定义查找的范围 [left,right]，初始查找范围是整个数组。每次取查找范围的中点 mid，比较 nums[mid] 和 target 的大小，如果相等则 mid 即为要寻找的下标，如果不相等则根据 nums[mid] 和 target 的大小关系将查找范围缩小一半。

关键点：

搜索区间：注意区间的开闭，是否满足定义
循环不变量：最终搜索子区间，及之后退出循环的left、right指向位置

简单场景：单target查找

以leetcode-704为例：

搜索区间：左闭右闭

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 标准写法
def search(self, nums: List[int], target: int) -> int:
    left = 0
    # 搜索区间：[left,right]
    right = len(nums) - 1

    while left <= right:
        mid = (left+right)//2
        if nums[mid] < target:
            left = mid + 1
        elif nums[mid] > target:
            right = mid - 1
        else:
            return mid
    return -1

这里因为定义搜索区间为左闭右闭，所以：

left、right初始值毫无疑问
最终搜索子区间索引为：[i,i]
while循环作为子区间搜索，索引子区间[i,i]肯定属于搜索区间，所以判断条件为<=
当nums[mid] < target时，已知条件是target肯定在右边，但为什么不能更新为left = mid，是因为考虑到缩小到的子区间里可能有mid==left情况，此时如果不+1移动更新区间，就是死循环；right值处理跟left类似所以只要在mid==left时更新区间，其实也可能设置为mid，因为[mid, right]也是符合条件的搜索区间，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


# 其他写法
def search(self, nums: List[int], target: int) -> int:
    left = 0
    right = len(nums) - 1

    while left <= right:
        mid = (left+right)//2
        if nums[mid] < target:
            if mid == left:
                left = mid + 1
            else:
                # 不为mid+1也没问题，不过部分子区间重复搜索
                left = mid
        elif nums[mid] > target:
            if mid == left:
                right = mid - 1
            else:
                right = mid
        else:
            return mid
    return -1

搜索区间：左闭右开

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 标准写法
def search(self, nums: List[int], target: int) -> int:
    left = 0
    # 搜索区间：[left,right)
    right = len(nums)

    while left < right:
        mid = (left+right)//2
        if nums[mid] < target:
            left = mid + 1
        elif nums[mid] > target:
            right = mid
        else:
            return mid
    return -1

这里因为定义搜索区间为左闭右开，所以：

left、right初始值毫无疑问
最终搜索子区间索引为：[i,i+1]
while循环作为子区间搜索，索引子区间[i,i]不属于搜索区间，所以判断条件为<
当nums[mid] < target时，但为什么不能更新为left = mid，和上面类似；当nums[mid] > target时，则已知最小可搜索空间为[left,mid)，当然也可以为[left,mid+i)（mid<=mid+i<=right），但这就多了许多重复搜索所以只要在mid==left时更新区间，其实也可能设置为mid，因为[mid, right]也是符合条件的搜索区间，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


# 其他写法
def search(self, nums: List[int], target: int) -> int:
    left = 0
    # 搜索区间：[left,right)
    right = len(nums)

    while left < right:
        mid = (left+right)//2
        if nums[mid] < target:
            if mid == left:
                left = mid + 1
            else:
                left = mid
        elif nums[mid] > target:
            right = mid
        else:
            return mid
    return -1

搜索区间：左开右开

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 标准写法
def search(self, nums: List[int], target: int) -> int:
    left = -1
    # 搜索区间：(left,right)
    right = len(nums)

    while left + 1 < right:
        mid = (left+right)//2
        if nums[mid] < target:
            left = mid
        elif nums[mid] > target:
            right = mid
        else:
            return mid
    return -1

原因和前两个类似，这里：

最终搜索子区间索引为：[i,i+1,i+2]

利用二分性质：第一个或最后一个target位置

以leetcode-34为例，定义搜索空间为左闭右闭：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


# 搜索第一个target位置
def lowerBound(nums, target):
    left = 0
    right = len(nums) - 1

    while left <= right:
        mid = (left + right)//2
        if nums[mid] < target:
            left = mid + 1
        # 等于情况移动right：不断将子搜索区间移动到小于target的第一个位置
        else:
            right = mid - 1
    return left

def searchRange(self, nums: List[int], target: int) -> List[int]:
    first_pos = lowerBound(nums, target)
    # 找不到target情况
    if first_pos == len(nums) or nums[first_pos] != target:
        return [-1, -1]
    end_pos = lowerBound(nums, target+1) - 1
    return [first_pos, end_pos]

上面的nums[mid] == target情况修改为移动left：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


def lowerBound(nums, target):
    left = 0
    right = len(nums) - 1

    while left <= right:
        mid = left + (right - left)//2
        # 等于情况移动left：不断将子搜索区间移动大于target的第一个位置
        if nums[mid] <= target:
            left = mid + 1
        else:
            right = mid - 1
    return left

def searchRange(self, nums: List[int], target: int) -> List[int]:
    first_pos = lowerBound(nums, target)
    # 找不到target情况
    if first_pos == 0 or nums[first_pos-1] != target:
        return [-1, -1]
    end_pos = lowerBound(nums, target-1)
    return [end_pos, first_pos-1]

总结

由上可以总结如下：

二分查找在mid和target值相等时，继续移动区间，则在有多个target值的情况时：
1、相等时移动right，最终结果为等于target的第一个位置
2、相等时移动left，最终结果为大于target的第一个位置

注意

但当相等情况复杂时，如果相等位置切分不当，left最终位置可能与预期位置不一致，可以通过以leetcode-33为例思考。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


def search(self, nums: List[int], target: int) -> int:
    def moveLeft(i):
        end = nums[-1]
        if nums[i] > end:
            return target >= nums[i] or target <= end
        else:
            return target >= nums[i] and target <= end
    left = 0
    right = len(nums) - 1
    while left <= right:
        mid = (left+right)//2
        # 如果相等情况不return mid，则moveLeft判断就需要进行仔细考虑该场景下相等情况子区间的移动
        if nums[mid] == target:
            return mid
        elif moveLeft(mid):
            left = mid+1
        else:
            right=mid-1
            
    if left == len(nums) or nums[left] != target:
        return -1
    return left

局部可二分

以leetcode-162为例，定义搜索空间为左闭右闭：

为什么可以使用二分

简单证明：

我们可以以下标为x轴，元素值为y轴，在平面直角坐标系里绘制出每个元素的位置，再以直线连接，这样构成了一副折线图。由于题目保证两边界之外的元素为负无穷，相邻值不相等且至少存在一个非负无穷元素，所以必然有峰。那么我们任取相邻两点为m、m+1，则如果nums[m]<nums[m+1]，那么m+i, i=1,2..范围肯定存在一个该范围的最大值且为峰顶，同理，如果小于，那么反方向也肯定存在一个该范围的最大值且为峰顶。因而可以用二分解决。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def findPeakElement(self, nums: List[int]) -> int:
    left = 0
    right = len(nums) - 2 # 忽略末尾元素，防止越界
    # 或者这样处理
    # right = len(nums) - 1
    # nums.append(-inf)
    while left <= right:
        mid = (left+right)//2
        if nums[mid] > nums[mid+1]:
            right = mid - 1
        else:
            left = mid + 1
    return left

回溯

概念

回溯法就是暴力解法。其基本思想是通过遍历每个阶段的所有可能选择，从而获得想要的所有可能，通常使用递归实现。并且通常从第一步开始选择，到最后一步结束，所以呈现类似对树进行DFS的操作，每层代表着每一步，从上往下的每个节点代表着累积的选择。

递阶段：每次递的过程代表了每步进行了一种选择，递操作结束时代表所有步都做出了一种选择。
归阶段：每次归的过程往往伴随着撤销操作，代表对上一个选择的放弃，归操作结束时代表撤销所有步的所有选择。

关键点：

递阶段：考虑当前步的所有选择，可通过条件进行剪枝。每步的选择可分为关联选择和无关选择。
- 关联选择：步与步之间的选择是有关联关系的，某步选了，其他步就会有约束（如不能选）；
- 无关选择：步与步之间的选择互不干扰，不受其他步的约束。
递结束：当前所有步的选择结果是否符合
归阶段：注意撤销之前选择
其他：
- 选择约束：某步的选择有约束，如可以不选、必须选或不能重复选等
- 递结束条件：需要多少步等

无关选择类型

以leetcode-17为例：

无关选择：每步的选择与其他步不相关
递结束条件：步数为digits长度
选择约束：每步的所有选择必须选一个

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


def letterCombinations(self, digits: str) -> List[str]:
    if not digits:
        return []
    ans = []
    # 存储每步的选择
    paths = []
    num2char = {
        '1': "", '2': "abc", '3': "def",
        '4': "ghi", '5': "jkl", '6': "mno",
        '7': "pqrs", '8': "tuv", '9': "wxyz"
    }

    def dfs(i):
        # 已经走完最后一步
        if i==len(digits):
            ans.append("".join(paths))
            return
        
        # 遍历所有选择，选择之间无关联
        for c in num2char[digits[i]]:
            # 作出当前步的选择，往下递
            paths.append(c)
            dfs(i+1)
            # 归时撤销之前选择
            paths.pop()
    
    # 从第一步开始
    dfs(0)
    return ans

关联选择类型

以leetcode-78为例：

关联选择：每步的选择与其他步相关
递结束条件：步数为k
满足结果条件：选择为组合不重复，非排列
选择约束：每步的选择为前面选择后剩下的，且必须选一个

简单粗暴，但超时，因为去重和修改每步选择的实现耗时严重

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


def combine(self, n: int, k: int) -> List[List[int]]:
    ans = set()
    paths = []

    def dfs(i, choice):
        if i==k:
            # 满足结果条件，去除重复
            ans.add(tuple(sorted(paths)))
            return
        
        for index in range(len(choice)):
            new_choice=choice.copy()
            # 缩小下一步可用选择
            del new_choice[index]
            paths.append(choice[index])
            dfs(i+1, new_choice)
            paths.pop()
    
    dfs(0, [i for i in range(1,n+1)])
    return [list(item) for item in ans]

优化：修改每步选择的实现，加入结果条件的约束

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


def combine(self, n: int, k: int) -> List[List[int]]:
    ans = []
    paths = []
    choices = [i for i in range(1,n+1)] # 所有选择
    mask = [True for _ in range(n)] # dfs实现，所以一个数组即可记录一条路径上的选择结果

    def dfs(i):
        if i==k:
            ans.append(paths.copy())
            return
        
        for j in range(len(choices)):
            # 选择是否可用
            if mask[j]:
                # 添加满足结果条件约束
                if len(paths) >0:
                    # 严格递增的选择，上一步的选择比当前大，证明已经遍历过该选择
                    if choices[j] < paths[-1]:
                        continue
                paths.append(choices[j])
                # 额外对选择进行标记
                mask[j]=False
                dfs(i+1)
                paths.pop()
                # 选择其他时进行回退
                mask[j]=True
    
    dfs(0)
    return ans

根据满足结果条件进行优化：注意到结果为其实为选择的排列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


def combine(self, n: int, k: int) -> List[List[int]]:
    ans = []
    paths = []
    choices = [i for i in range(1,n+1)]

    def dfs(i):
        # 这里第几步不是用i表示，而是paths长度，i表示上一步选择的位置
        if len(paths)==k:
            ans.append(paths.copy())
            return
        # 从之前选择位置往后选
        for j in range(i, len(choices)):
            paths.append(choices[j])
            dfs(j+1)
            paths.pop()
    
    dfs(0)
    return ans

同理，leetcode-51

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


def solveNQueens(self, n: int) -> List[List[str]]:
    ans = []
    if n == 0:
        return ans
    # 注意这里不能写成（行引用，非n个独立list）：[["."] *n] * n
    paths = [["."] *n for _ in range(n)]
    column = [False] * n
    ldiag = [False] * (2 * n - 1)  # 左对角线
    rdiag = [False] * (2 * n - 1)  # 右对角线

    def dfs(row):
        if row == n:
            ans.append(["".join(item) for item in paths])
            return
        
        for i in range(n):
            # 难点：注意到结果要满足的条件
            if column[i] or ldiag[n - row + i - 1] or rdiag[row + i]:
                continue
            
            paths[row][i] = 'Q'
            column[i] = ldiag[n - row + i - 1] = rdiag[row + i] = True
            dfs(row + 1)
            paths[row][i] = '.'
            column[i] = ldiag[n - row + i - 1] = rdiag[row + i] = False

    dfs(0)
    return ans

动态规划

动态规划的定义

动态规划（Dynamic Programming）：简称 DP，是一种求解多阶段决策过程最优化问题的方法。在动态规划中，通过把原问题分解为相对简单的子问题，先求解子问题，再由子问题的解而得到原问题的解。

动态规划最早由理查德 · 贝尔曼于 1957 年在其著作「动态规划（Dynamic Programming）」一书中提出。这里的 Programming 并不是编程的意思，而是指一种「表格处理方法」，即将每一步计算的结果存储在表格中，供随后的计算查询使用。

动态规划的核心思想

动态规划的核心思想：

把「原问题」分解为「若干个重叠的子问题」，每个子问题的求解过程都构成一个 「阶段」。在完成一个阶段的计算之后，动态规划方法才会执行下一个阶段的计算。

在求解子问题的过程中，按照「自顶向下的记忆化搜索方法」或者「自底向上的递推方法」求解出「子问题的解」，把结果存储在表格中，当需要再次求解此子问题时，直接从表格中查询该子问题的解，从而避免了大量的重复计算。

这看起来很像是分治算法，但动态规划与分治算法的不同点在于：

适用于动态规划求解的问题，在分解之后得到的子问题往往是相互联系的，会出现若干个重叠子问题。
使用动态规划方法会将这些重叠子问题的解保存到表格里，供随后的计算查询使用，从而避免大量的重复计算。

动态规划的特征

究竟什么样的问题才可以使用动态规划算法解决呢？

首先，能够使用动态规划方法解决的问题必须满足以下三个特征：

最优子结构性质
重叠子问题性质
无后效性

最优子结构性质

最优子结构：指的是一个问题的最优解包含其子问题的最优解。

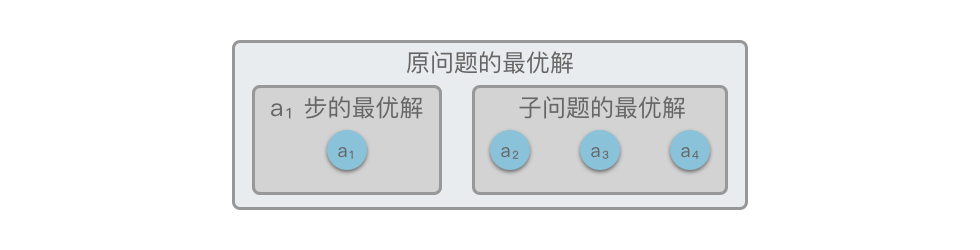
举个例子，如下图所示，原问题 $S = \lbrace a_1, a_2, a_3, a_4 \rbrace$，在 $a_1$ 步我们选出一个当前最优解之后，问题就转换为求解子问题 $S_{\text{子问题}} = \lbrace a_2, a_3, a_4 \rbrace$。如果原问题 $S$ 的最优解可以由「第 $a_1$ 步得到的局部最优解」和「 $S_{\text{子问题}}$ 的最优解」构成，则说明该问题满足最优子结构性质。

也就是说，如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质。

最优子结构性质

重叠子问题性质

重叠子问题性质：指的是在求解子问题的过程中，有大量的子问题是重复的，一个子问题在下一阶段的决策中可能会被多次用到。如果有大量重复的子问题，那么只需要对其求解一次，然后用表格将结果存储下来，以后使用时可以直接查询，不需要再次求解。

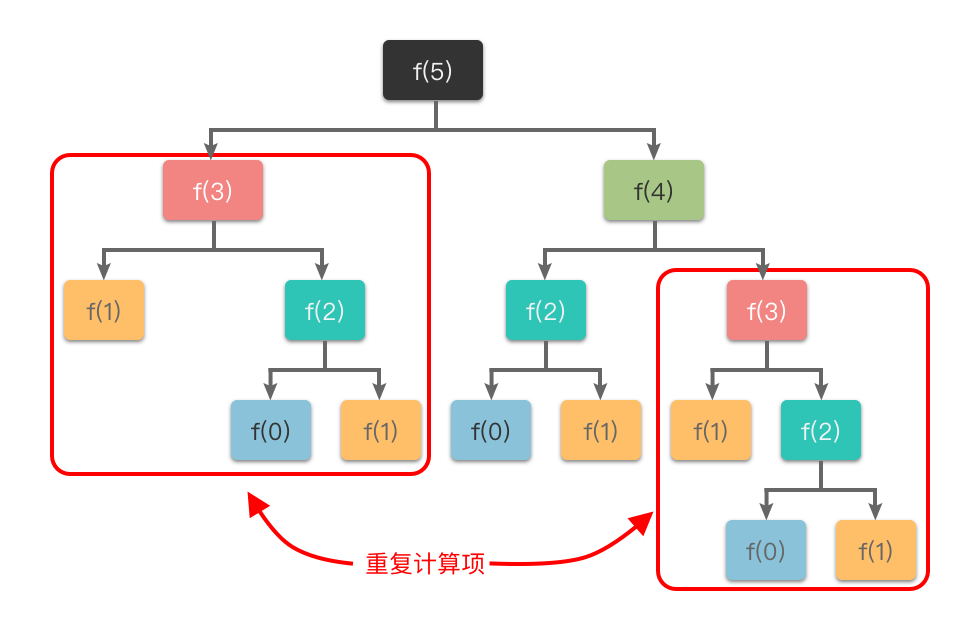
重叠子问题性质

之前我们提到的「斐波那契数列」例子中，$f(0)$、$f(1)$、$f(2)$、$f(3)$ 都进行了多次重复计算。动态规划算法利用了子问题重叠的性质，在第一次计算 $f(0)$、$f(1)$、$f(2)$、$f(3)$ 时就将其结果存入表格，当再次使用时可以直接查询，无需再次求解，从而提升效率。

无后效性

无后效性：指的是子问题的解（状态值）只与之前阶段有关，而与后面阶段无关。当前阶段的若干状态值一旦确定，就不再改变，不会再受到后续阶段决策的影响。

也就是说，一旦某一个子问题的求解结果确定以后，就不会再被修改。

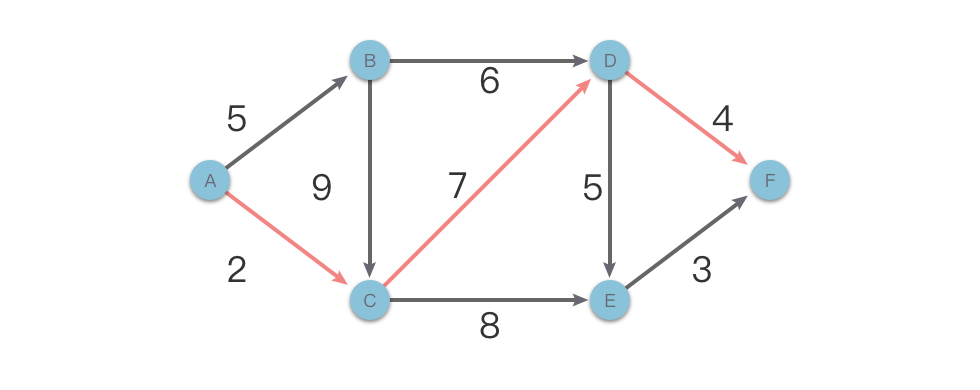
举个例子，下图是一个有向无环带权图，我们在求解从 $A$ 点到 $F$ 点的最短路径问题时，假设当前已知从 $A$ 点到 $D$ 点的最短路径（$2 + 7 = 9$）。那么无论之后的路径如何选择，都不会影响之前从 $A$ 点到 $D$ 点的最短路径长度。这就是「无后效性」。

而如果一个问题具有「后效性」，则可能需要先将其转化或者逆向求解来消除后效性，然后才可以使用动态规划算法。

无后效性

动态规划的基本思路

如下图所示，我们在使用动态规划方法解决某些最优化问题时，可以将解决问题的过程按照一定顺序（时间顺序、空间顺序或其他顺序）分解为若干个相互联系的「阶段」。然后按照顺序对每一个阶段做出「决策」，这个决策既决定了本阶段的效益，也决定了下一阶段的初始状态。依次做完每个阶段的决策之后，就得到了一个整个问题的决策序列。

这样就将一个原问题分解为了一系列的子问题，再通过逐步求解从而获得最终结果。

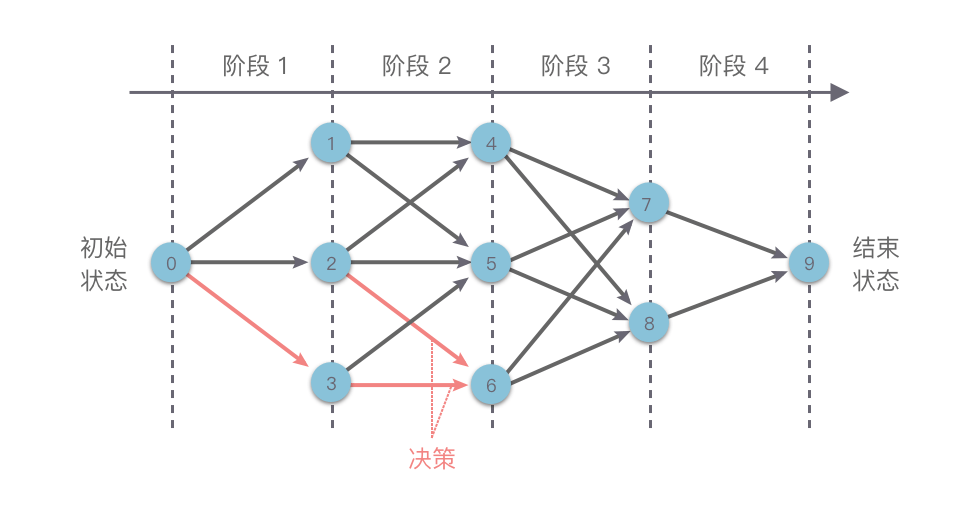
动态规划方法

这种前后关联、具有链状结构的多阶段进行决策的问题也叫做「多阶段决策问题」。

通常我们使用动态规划方法来解决问题的基本思路如下：

划分阶段：将原问题按顺序（时间顺序、空间顺序或其他顺序）分解为若干个相互联系的「阶段」。划分后的阶段⼀定是有序或可排序的，否则问题⽆法求解。
- 这里的「阶段」指的是⼦问题的求解过程。每个⼦问题的求解过程都构成⼀个「阶段」，在完成前⼀阶段的求解后才会进⾏后⼀阶段的求解。
定义状态：将和子问题相关的某些变量（位置、数量、体积、空间等等）作为一个「状态」表示出来。状态的选择要满⾜⽆后效性。
- 一个「状态」对应一个或多个子问题，所谓某个「状态」下的值，指的就是这个「状态」所对应的子问题的解。
状态转移：根据「上一阶段的状态」和「该状态下所能做出的决策」，推导出「下一阶段的状态」。或者说根据相邻两个阶段各个状态之间的关系，确定决策，然后推导出状态间的相互转移方式（即「状态转移方程」）。
初始条件和边界条件：根据问题描述、状态定义和状态转移方程，确定初始条件和边界条件。
最终结果：确定问题的求解目标，然后按照一定顺序求解每一个阶段的问题。最后根据状态转移方程的递推结果，确定最终结果。

实现及优化思路

通常思路：

先确定每次操作及选择（子问题）
确定状态转移方程和初始值
用递归实现（逆向）
用数组（形状：n * choices）存储状态，改为循环实现（正向）
根据状态转移方程确定子问题关联了多少步的状态，从而优化空间

关键点：

子问题
状态转移方程
初始值（满足条件和不满足条件）

0-1背包

概念

有 n 个物品，第 i 个物品的体积为 w[i] ，价值为 v[i] 。
每个物品至多选一个，求体积和不超过 capacity 时的最大价值和。

注意点：

当前操作？枚举第 $ i $ 个物品选或不选：
- 不选，剩余容量不变；
- 选，剩余容量减少 $ w[i] $。
子问题？在剩余容量为 $ c $ 时，从 前 $ i $ 个物品 中得到的最大价值和。
下一个子问题？分类讨论：
- 不选：在剩余容量为 $ c $ 时，
  从 前 $ i-1 $ 个物品 中得到的最大价值和。
- 选：在剩余容量为 $ c - w[i] $ 时，
  从 前 $ i-1 $ 个物品 中得到的最大价值和。
回溯思考：有n步，每步有两种选择。

递归公式：

$$ dfs(i, c) = \max(dfs(i-1, c), dfs(i-1, c - w[i]) + v[i]) $$

例子

以leetcode-494为例：

回溯实现，python超时，C++通过

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


def findTargetSumWays(self, nums: List[int], target: int) -> int:
    ans = [0]
    n = len(nums)

    def dfs(i, t):
        if i == n:
            if t == target:
                ans[0] += 1
            return
        # 每步可选'+'或'-'
        dfs(i+1, t-nums[i])
        dfs(i+1, t+nums[i])

    dfs(0, 0)
    return ans[0]

动态规划

注意到：所求方案中的负数和或正数和与总和及target值相关，可转换为0-1背包问题进行求解
状态转移方程：$dfs(i,c)=dfs(i-1,c)+dfs(i-1,c-nums[i])$
dfs(i,c)含义：前i个和为c的方案数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79


# 递归形式
def findTargetSumWays(self, nums: List[int], target: int) -> int:
    target += sum(nums)
    # 数学约束，保证target存在
    if target < 0 or target % 2 != 0:
        return 0
    target //=2
    n = len(nums)

    @cache
    def dfs(i, t):
        if i<0:
            if t==0:
                return 1
            return 0
        if nums[i] > t:
            return dfs(i-1, t)
        return dfs(i-1, t) + dfs(i-1, t-nums[i])
    
    return dfs(n-1, target)

# 数组形式
def findTargetSumWays(self, nums: List[int], target: int) -> int:
    target += sum(nums)
    if target < 0 or target % 2 != 0:
        return 0
    target //=2
    n = len(nums)
    # 动态转移方程改为 dfs(i+1,c)=dfs(i,c)+dfs(i,c-nums[i])
    dfs = [[0]*(target+1) for _ in range(n+1)]
    # dfs[0][0]表示最后一轮且c-nums[i]刚好为0
    # 其实dfs[i][0]都应该初始化为1，但下面c < nums[i]操作肯定会执行进行拷贝，所以只用初始化第一个
    dfs[0][0] = 1
    for i in range(n):
        # 这里遍历范围为target+1，保证n步都能满足
        for c in range(target+1):
            if c < nums[i]:
                dfs[i+1][c] = dfs[i][c]
            else:
                dfs[i+1][c] = dfs[i][c]+dfs[i][c-nums[i]]
    return dfs[n][target]

# 数组形式可优化空间，由状态转移方程可以知道：某一状态只会用到前一个状态的结果，所以只需要两个数组即可
def findTargetSumWays(self, nums: List[int], target: int) -> int:
    target += sum(nums)
    if target < 0 or target % 2 != 0:
        return 0
    
    target //=2
    n = len(nums)
    # 两个数组存储，空间 O(target)
    dfs = [[0]*(target+1) for _ in range(2)]
    dfs[0][0] = 1
    # 用cur，next标记当前状态和下一个状态，也可用取模操作，但取模操作耗时高
    cur, next = 0, 1
    for i in range(n):
        for c in range(target+1):
            if c < nums[i]:
                dfs[next][c] = dfs[cur][c]
            else:
                dfs[next][c] = dfs[cur][c]+dfs[cur][c-nums[i]]
        cur, next = next, cur
    return dfs[cur][target]

# 注意到：下一次的状态其实只需要当前的两个位置的状态结果c和c-nums[i]，nums[i]非负，所以可用一个数组逆序转移
def findTargetSumWays(self, nums: List[int], target: int) -> int:
    target += sum(nums)
    if target < 0 or target % 2 != 0:
        return 0
    
    target //=2
    n = len(nums)
    dfs = [0]*(target+1)
    dfs[0] = 1
    for x in nums:
        for c in range(target, -1, -1):
            if c >= x:
                dfs[c] = dfs[c]+dfs[c-x]
    return dfs[target]

完全背包

概念

有 $ n $ 种物品，第 $ i $ 种物品的体积为 $ w[i] $，价值为 $ v[i] $。
每种物品 无限次重复 选，求体积和不超过 $ capacity $ 时的最大价值和。

注意点：

当前操作？枚举第 $ i $ 种物品选一个或不选：
- 不选，剩余容量不变；
- 选一个，剩余容量减少 $ w[i] $。
子问题？在剩余容量为 $ c $ 时，从 前 $ i $ 种物品 中得到的最大价值和。
下一个子问题？分类讨论：
- 不选：在剩余容量为 $ c $ 时，从 前 $ i-1 $ 种物品 中得到的最大价值和。
- 选一个：在剩余容量为 $ c - w[i] $ 时，从 前 $ i $ 种物品 中得到的最大价值和。

递归公式：

$$ dfs(i, c) = \max(dfs(i-1, c), dfs(i, c - w[i]) + v[i]) $$

例子

以leetcode-322为例

不同于0-1背包某个物品只能选一次
这里要求最小数量：修改转移方程和不满足时返回值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


# 递归实现
def coinChange(self, coins: List[int], amount: int) -> int:
    @cache
    def dfs(i, c):
        if i<0:
            if c==0:
                return 0
            return inf
        if coins[i] > c:
            return dfs(i-1, c)
        return min(dfs(i-1, c), dfs(i, c-coins[i])+1)
    ans = dfs(len(coins)-1, amount)
    return ans if ans < inf else -1
# 和上一题同理，改为数组+空间优化
def coinChange(self, coins: List[int], amount: int) -> int:
    n = len(coins)
    dfs = [inf]*(amount+1)
    dfs[0]=0
    for x in coins:
        for c in range(amount+1):
            if c>=x:
                dfs[c] = min(dfs[c], dfs[c-x]+1)
    ans = dfs[amount]
    return ans if ans < inf else -1