References
- 深度神经网络剪枝综述,A Survey on Deep Neural Network Pruning: Taxonomy, Comparison, Analysis, and Recommendations
- 目前针对大模型剪枝的方法有哪些?
- MIT 6.5940 TinyML and Efficient Deep Learning Computing
- 模型压缩的小白入门教程
介绍
**模型剪枝(Model Pruning)**是一种用于减少神经网络模型参数数量和计算量的技术。它通过识别和去除在训练过程中对模型性能影响较小的参数或连接,从而实现模型的精简和加速。
通常,模型剪枝可以分为两种类型:结构化剪枝(Structured Pruning)和非结构化剪枝(Unstructured Pruning)。
结构化剪枝和非结构化剪枝的主要区别在于剪枝目标和由此产生的网络结构。结构化剪枝根据特定规则删除连接或层结构,同时保留整体网络结构。而非结构化剪枝会剪枝各个参数,从而产生不规则的稀疏结构。
模型剪枝的一般步骤包括:
- 训练初始模型:首先,需要训练一个初始的大模型,通常是为了达到足够的性能水平。
- 评估参数重要性:使用某种评估方法(如:权重的绝对值、梯度信息等)来确定模型中各个参数的重要性。
- 剪枝:根据评估结果,剪枝掉不重要的参数或连接,可以是结构化的或非结构化的。
- 修正和微调:进行剪枝后,需要进行一定的修正和微调,以确保模型的性能不会显著下降。
模型剪枝可以带来多方面的好处,包括减少模型的存储需求、加速推理速度、减少模型在边缘设备上的资源消耗等。然而,剪枝可能会带来一定的性能损失,因此需要在剪枝前后进行适当的评估和调整。
剪枝方法
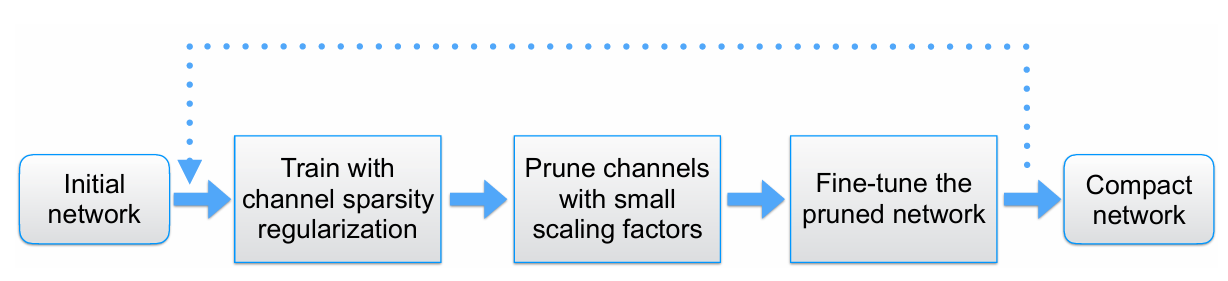
Network Slimming
基本思想
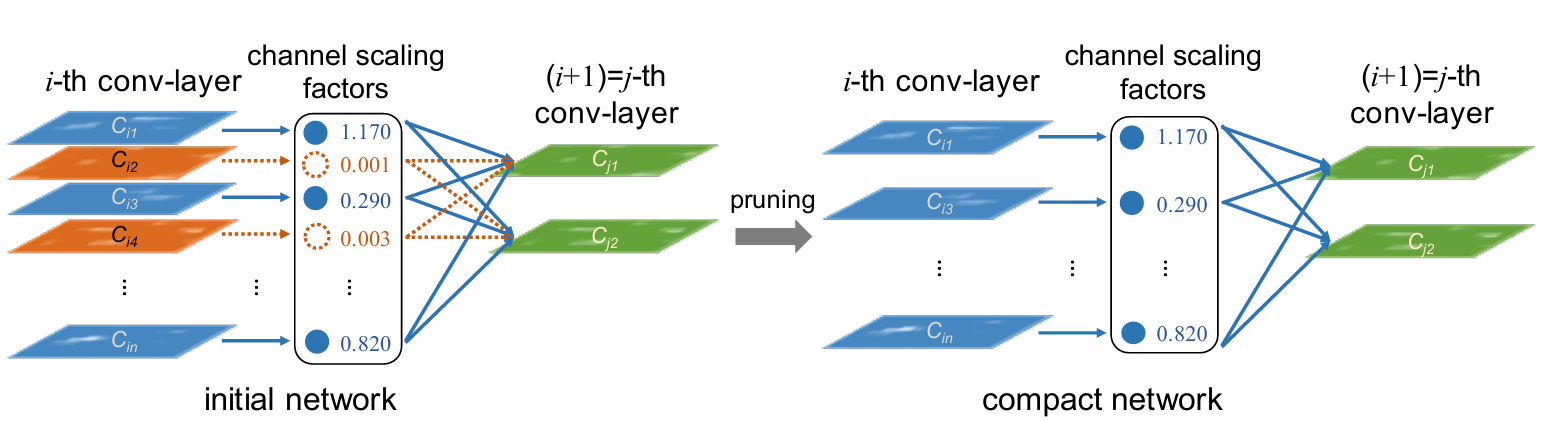
论文核心点
- 以 BN 中的 γ 为切入点,即 γ 越小,其对应的特征图越不重要
- 为了使得 γ 能有特征选择的作用,引入 L1 正则来控制 γ $$ L = \sum_{(x,y)} l(f(x, W), y) + \lambda \sum_{\gamma \in \Gamma} g(\gamma) $$
BatchNorm
如何得到每个特征图的重要性呢?–BN要解决的问题
- Network slimming,就是利用BN层中的缩放因子Y
- 先来回顾下BN是做什么的:$\hat{x}^{(k)} = \frac{x^{(k)} - E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}$
- 整体感觉就是一个归一化操作,但是BN中还额外引入了两个可训练的参数:γ和β。
BN本质作用
- BN要做的就是把越来越偏离的分布给他拉回来!
- 再重新规范化到均值为0方差为1的标准正态分布
- 这样能够使得激活函数在数值层面更敏感,训练更快
- 有一种感觉:经过BN后,把数值分布强制在了非线性函数的线性区域中
BN额外参数
- 如果都是线性的了,神经网络还有意义吗?
- BN另一方面还需要保证一些非线性,对规范化后的结果再进行变换
- 这两个参数是训练得到的:$y^{(k)}=\gamma^{(k)}\hat{x}^{(k)}+\beta^{(k)}$
- 感觉就是从正太分布进行一些改变,拉动一下,变一下形状!
稀疏化原理与效果
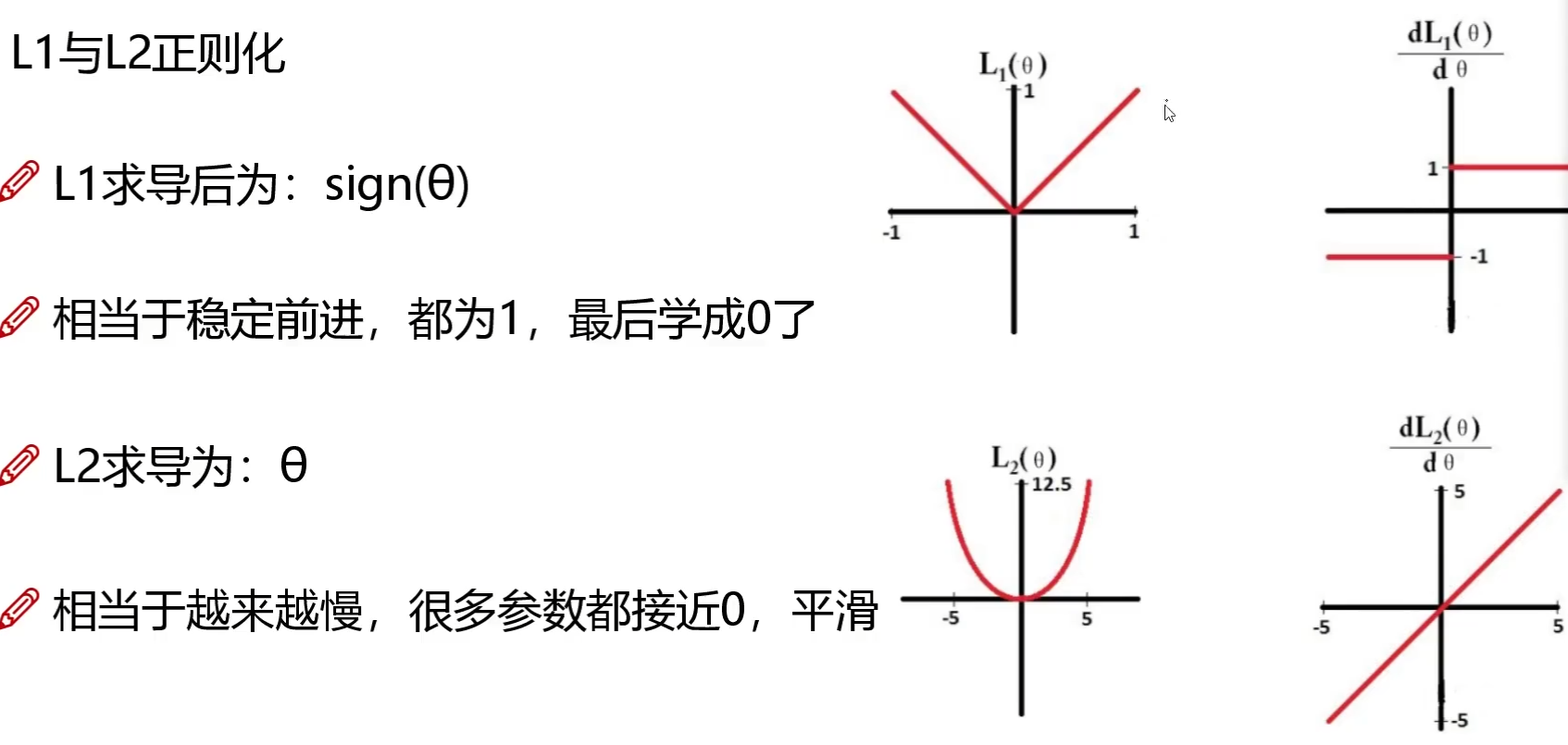
- 论文中提出:训练时使用 L1 正则化能对参数进行稀疏作用
- L1:稀疏与特征选择;L2:平滑特征
- L1 正则化:$J(\vec{\theta}) = \frac{1}{2} \sum_{i=1}^{m} \left( h_{\vec{\theta}}(x^{(i)}) - y^{(i)} \right)^2 + \lambda \sum_{j=1}^{n} |\theta_j|$,$\theta_j$是要正则化的参数
- L2 正则化:$J(\vec{\theta}) = \frac{1}{2} \sum_{i=1}^{m} \left( h_{\vec{\theta}}(x^{(i)}) - y^{(i)} \right)^2 + \lambda \sum_{j=1}^{n} \theta_j^2$,同上
剪枝流程